206 - Radiation Hardness Edit Page
Contents
Radiation Hardness
NIEL
The particle energy deposition mechanisms by ionization and non-ionization processes are reviewed as well as the radiation-induced damage and its effect on device parameters evolution, depending on particle type, energy and fluence. The temporary or permanent damage inflicted by a single particle (single event effect) to electronic devices or integrated circuits is treated separately from the total ionizing dose (TID) effect for which the accumulated fluence causes degradation and from the displacement damage induced by the non-ionizing energy-loss (NIEL) deposition. Under most of radiation level of collider detector, the NIEL dominants decrease of detector performance. Here introduce the NIEL hypothesis which normalize the value from one particle to another, or from one energy to another for the same type particle.[1]
The Non Ionising Energy Loss NIEL hypothesis allows a first-order normalization of radiation damage with respect to different particles or particles with different energy.According to NIEL, the damage manifestation depends only on energy transferred in collisions.
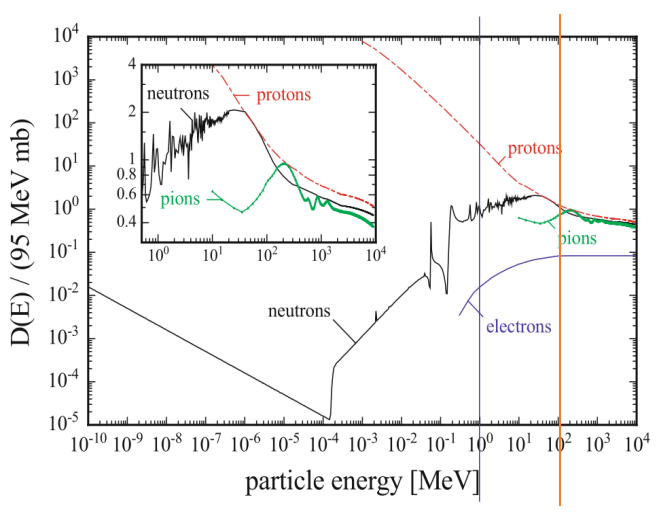
where \(\kappa\) is defined as the ratio of the individual damage particle factor for a given energy and 1 MeV neutrons; \(D(E)\) is displacement damage function; \(\Phi_{e q}\) is the 1 MeV neutron equivalent fluence; \(\Phi(E)\) is particle fluence with energy \(E\).
The 1 MeV neutron equivalent fluence s then calculated by
\[\Phi_{e q}=\kappa \Phi=\kappa \int \phi(E) d E ; \quad\left[\Phi_{e q}\right]=n_{1 \mathrm{MeV}} / \mathrm{cm}^{2}\]Such as 100 MeV proton equivalent fluences[3]
\[D(E=100 \mathrm{MeV})_{\text {proton }}=1.276 \times D(E=1 \mathrm{MeV})_{\text {neutron }}[95 \mathrm{MeV} \mathrm{mb}]\] \[\Phi_{\text {proton }}\left[n_{1MeV}/ c m^{2}\right]=\frac{\Phi_{\text {neutron }}}{1.276}\left[n_{1MeV}/ c m^{2}\right]\]Leakage Currents
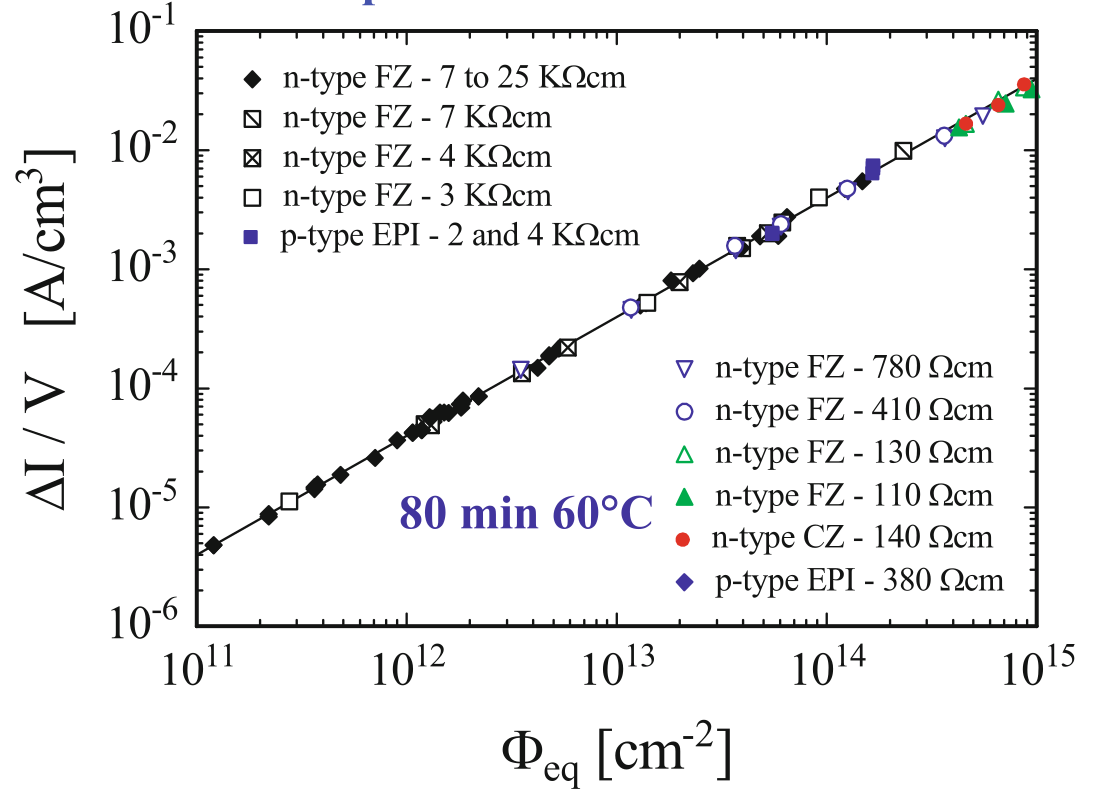
The defect levels close to the middle of the bandgap lead to an increase of the leakage current of silicon devices after irradiation. A linear behaviour of leakage current was found in many experiments:
\[\frac{\Delta I (\Phi_{eq})}{V} = \alpha \Phi_{eq}\]where \(V\) is active region volume, \(\Delta I = I(\Phi_{eq}) - I(unirradiated)\) is the leakage current increase caused by irradiation. \(\alpha\) is called the current-related damage rate. As Fig.2[4] shows the leakage current in various silicon detectors, \(\alpha=(3.99\pm0.03)\times10^{-17}\) A/cm which measurements taken at 20\(^{\circ}\)C after a standard annealing process 80min@60\(^{\circ}\)C.
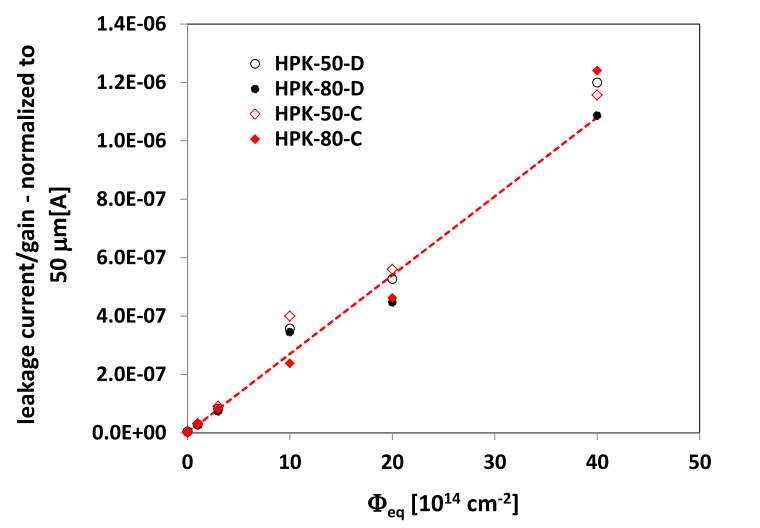
And for irradiated LGAD, the relation of leakage current should be corrected with internal gain:
\[\frac{\Delta I (\Phi_{eq})}{V} = \alpha \Phi_{eq} \times M_{I}(\Phi_{eq}, V_{bias})\]where \(M_{I}(\Phi_{eq}, V_{bias})\) is residual gain in irradiated LGAD. Fig.3[5] shows a good linear relation in measurements for irradiated LGAD based on corrected relation of leakage current.
Reference
[1] Leroy, C. , & Rancoita, P. G. . (2007). Particle interaction and displacement damage in silicon devices operated in radiation environments. Reports on Progress in Physics, volume 70(4), 493-625(133).(https://iopscience.iop.org/article/10.1088/0034-4885/70/4/R01/pdf)
[2] Hartmann, & F. (2009). Evolution of silicon sensor technology in particle physics. Springer Tracts in Modern Physics.(https://link.springer.com/book/10.1007/978-3-319-64436-3)
[3] NIEL data table: http://rd50.web.cern.ch/rd50/NIEL/default.html
[4] Moll M . Displacement Damage in Silicon Detectors for High Energy Physics[J]. IEEE Transactions on Nuclear Science, 2018, PP(99):1-1.(https://ieeexplore.ieee.org/document/8331152)
[5] G. Kramberger et al., “Radiation hardness of thin Low Gain Avalanche Detectors,” Nucl. Instrum.Methods A, vol. 891, pp. 68–77, 2018.(https://www.sciencedirect.com/science/article/pii/S0168900218301682)